Portas e Funções Lógicas

Portas lógicas são componentes fundamentais da eletrônica digital, responsáveis por realizar operações lógicas básicas em circuitos. Elas operam com valores binários (0 e 1), onde 0 representa o estado baixo ou falso, e 1 representa o estado alto ou verdadeiro. O resultado de uma porta lógica depende das entradas fornecidas e do tipo específico de operação lógica que a porta realiza.

AND

A porta AND pode ser representada pelo sinal de multiplicação, ou seja, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x e y sejam 1.

Representação matemática desse exemplo seria:

x * y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	0
1	0	0
0	1	0
1	1	1

Esboço da porta:

OR

A porta OR pode ser representada pelo sinal de adição, ou seja, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x ou y sejam 1.

Representação matemática desse exemplo seria:

x + y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	0
1	0	1
0	1	1
1	1	1

Esboço da porta:

NOT

A porta NOT pode ser representada pelo sinal de exclamação e representa a inversão, ou seja, supondo uma entrada x e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x seja 0.

Representação matemática desse exemplo seria:

!x = z

Representação do exemplo em uma tabela verdade:

x	z
0	1
1	0

Esboço da porta:

Observações:

• É possível representar a porta NOT colocando um traço em cima da variável que se deseja negar. Exemplo:

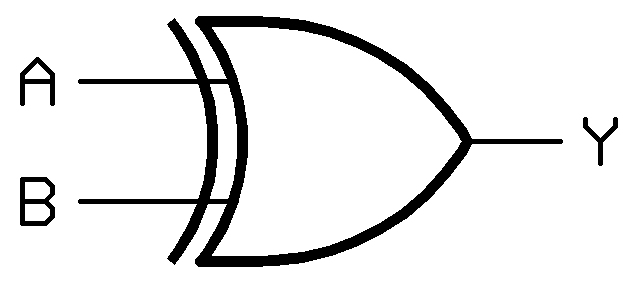
XOR

A porta XOR representa um "ou exclusivo". Desta forma, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x seja diferente de y, logo quando x = y = 1 ou x = y = 0 z retorna falso, ou z = 0.

Representação matemática desse exemplo seria:

x ⊕ y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	0
1	0	1
0	1	1
1	1	0

Esboço da porta:

Observações:

• É possível construir uma porta XOR usando portas AND, OR e NOT. A representação matemática seria desta forma:

  (!x * y) + (x * !y) = z

• Esboço usando portas AND, OR e NOT:

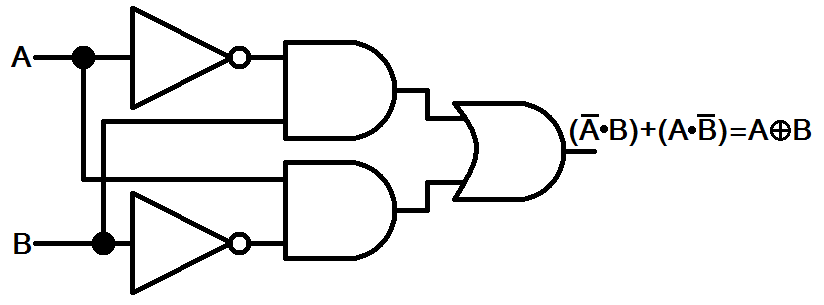
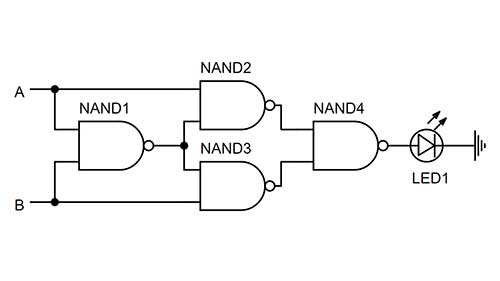
• É possível construir uma porta XOR usando somente portas NAND. Esboço usando somente portas NAND:

• Esboço de outra forma de construir uma porta XOR:

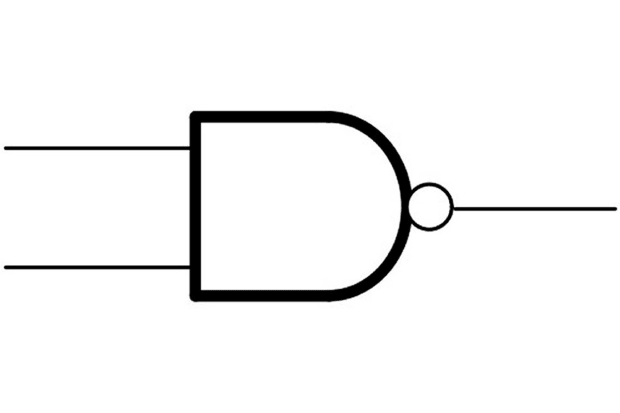
NAND

A porta NAND pode ser representado pela negação da porta lógica AND, ou seja, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x e y sejam diferentes de 1.

Representação matemática desse exemplo seria:

x ↑ y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	1
1	0	1
0	1	1
1	1	0

Esboço da porta:

NOR

A porta NOR pode ser representada pela negação da porta lógica OR, ou seja, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x ou y sejam diferentes de 1.

Representação matemática desse exemplo seria:

x ↓ y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	1
1	0	0
0	1	0
1	1	0

Esboço da porta:

XNOR

A porta XNOR, sendo um "ou exclusivo-não", representa a negação da porta lógica XOR. Desta forma, supondo duas entradas x e y e uma saída z, para a porta retornar verdadeiro, ou z = 1, é necessário que x seja igual ao y, logo quando x = y = 1 ou x = y = 0 z retorna verdadeiro, ou z = 1.

Representação matemática desse exemplo seria:

x ⊙ y = z

Representação do exemplo em uma tabela verdade:

x	y	z
0	0	1
1	0	0
0	1	0
1	1	1

Esboço da porta:

Exercícios

1. Faça esboços das portas lógicas aprendidas nesse capítulo.
2. Tente reproduzir as tabelas verdade de cada função.
3. Monte a tabela verdade do circuito abaixo:
4. Faça os exercícios de lógica booleana do capítulo seguinte, montando o desenho de cada circuito através das portas apresentadas nesse capítulo.

Contato

• Frederico Scheffel Oliveira - frederico.scheffel@usp.br
• Leonardo Massuhiro Sato - leonardo.m.sato@usp.br
• Pedro Henrique Perez Dias - pedro.perez@usp.br